The research program of our group is designed to explore the physics underlying the mechanical sensing capabilities of the auditory system. In particular, we are interested in determining how the system can respond to sub-nanometer deflections in an extremely rapid manner, how it maintains this sensitivity in the presence of noise, and how the higher-order processing centers in the brain control this sensitivity to protect the delicate hair cells from damage. The group combines experimental and theoretical approaches to unravel the physical processes underlying auditory neuroscience.
Research Program
Chaotic dynamics observed in hair bundle oscillations
Traditional theoretical models have described active dynamics of the auditory system as a system poised near a bifurcation. While these models capture many of the experimental phenomena, they include a fundamental tradeoff between the sensitivity of the system, which is aided by proximity to a critical point, and speed of response, which would then exhibit critical slowing down. As the auditory system exhibits extremely high temporal resolution, this tradeoff imposes an undesirable restriction. Furthermore, these models need extremely precise tuning of the cellular parameters to a particular point in phase space, which may be an unrealistic requirement for a biological system that must operate under various environmental stresses.
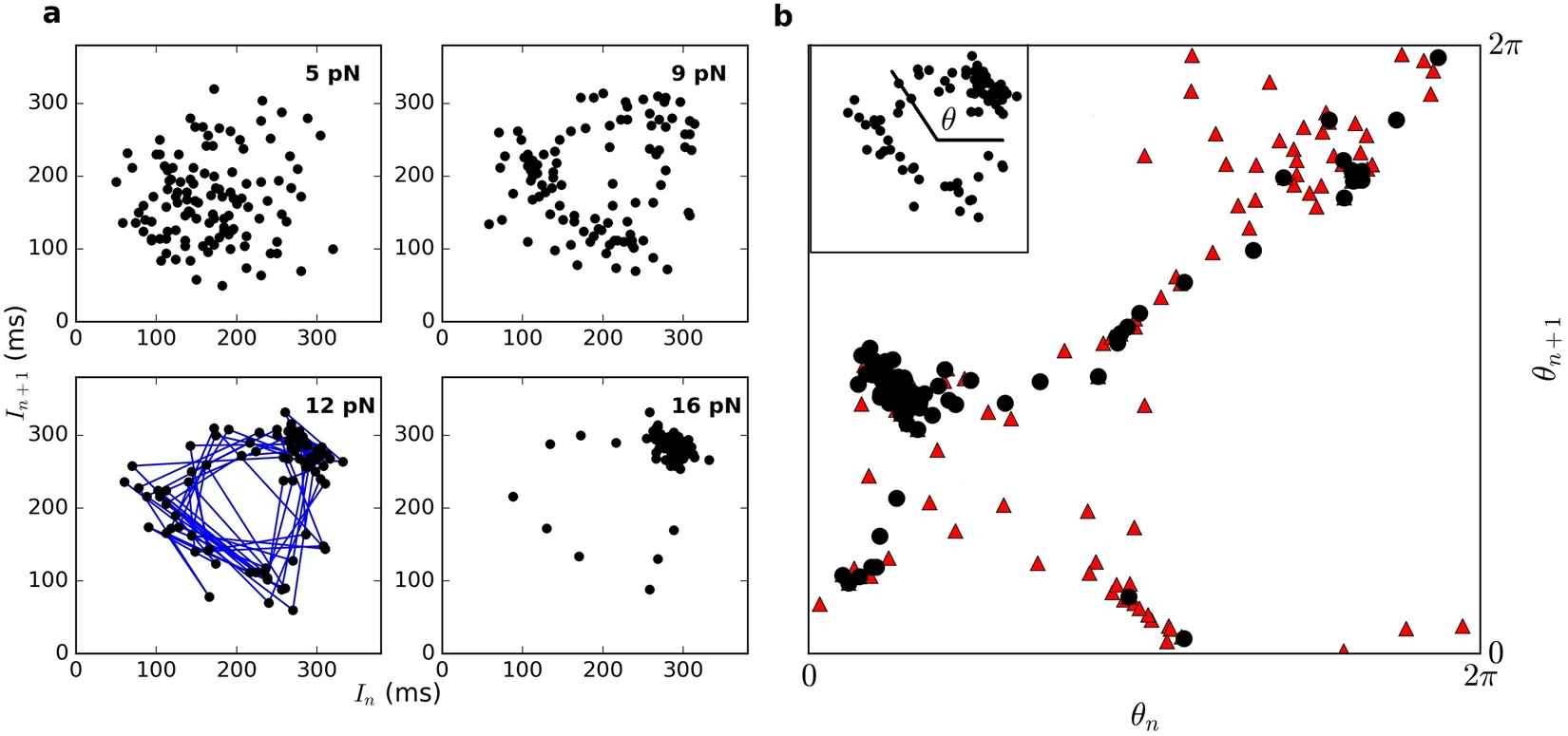 Figure 1. (a) Poincaré maps representing oscillations of
hair bundles driven by a sinusoidal stimulus below the resonance
frequency. Blue lines connect consecutive points in the series.
(b) Angles formed by vectors from the center of the ring
to each point in the Poincaré map (inset). Red and black points
represent data obtained for stimulus amplitudes of 9 pN and 12 pN,
respectively.
Figure 1. (a) Poincaré maps representing oscillations of
hair bundles driven by a sinusoidal stimulus below the resonance
frequency. Blue lines connect consecutive points in the series.
(b) Angles formed by vectors from the center of the ring
to each point in the Poincaré map (inset). Red and black points
represent data obtained for stimulus amplitudes of 9 pN and 12 pN,
respectively.
Chaos is characterized by dynamics that are extremely sensitive to perturbations, as even minute differences in the initial conditions lead to an exponential divergence of trajectories of the system. Further, its speed of response is set by the value of the Lyapunov exponent, and hence improves with chaoticity. Sensitivity of the auditory system to external perturbations raises the possibility that chaos may be exploited by hair cells in the detection of auditory signals. We are therefore exploring the presence of chaotic dynamics in hair bundle oscillations and the role it may play in enhancing the sensitivity and temporal resolution of detection.
Our recordings of spontaneous and driven hair bundle oscillations indicate the presence of a chaotic attractor. Poincaré maps of the oscillator, subject to varying amplitudes of external forcing, exhibited clear signatures of torus breakdown, which provides a rigorous test of chaotic dynamics (Figure 1). An assortment of additional analytical tools was used to confirm the presence of chaos in the innate and driven bundle motility.
Further, we developed a method of modulating the degree of chaos of hair cells, in vitro, by changing the conditions of the solution in which the cells are immersed. We then demonstrated experimentally that sensitivity to various stimulus waveforms is enhanced in the weakly chaotic regime. Further, we showed that the temporal resolution of the system’s response to an abrupt stimulus increases with increasing degrees of chaos. We supplemented the experiments with a theoretical model of hair bundle dynamics (Figure 2). The numerical simulations robustly reproduced the experimental results, indicating that weak chaos leads to optimal detection characteristics. Thus, we propose that chaotic dynamics are responsible for the extreme sensitivity and temporal resolution of the auditory and vestibular systems.
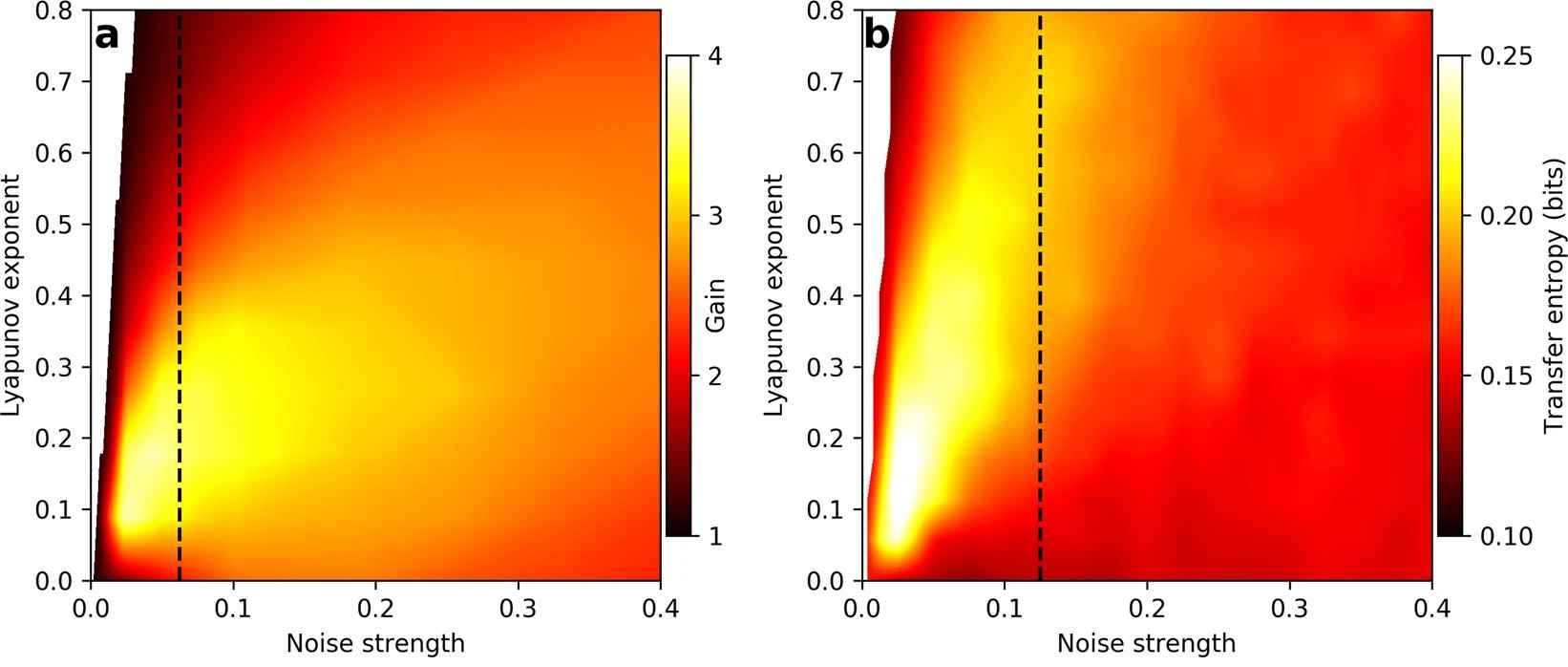 Figure 2. (a) Phase-locked amplitude gain for
on-resonance sinusoidal stimulus. (b) Transfer entropy
from burst noise stimulus to response of the Hopf oscillator. For
(a,b) Parameters were varied, resulting in a range of Lyapunov
exponents. The stimulus amplitude was fixed for both panels. The
vertical dashed lines indicate the points where the signal-to-noise
ratio is 1, as defined by the ratio of the signal power to the noise
power.
Figure 2. (a) Phase-locked amplitude gain for
on-resonance sinusoidal stimulus. (b) Transfer entropy
from burst noise stimulus to response of the Hopf oscillator. For
(a,b) Parameters were varied, resulting in a range of Lyapunov
exponents. The stimulus amplitude was fixed for both panels. The
vertical dashed lines indicate the points where the signal-to-noise
ratio is 1, as defined by the ratio of the signal power to the noise
power.
Efference and dynamic feedback control
Auditory detection requires not only the sensitivity to detect weak signals (as low as 0 dB), but also the ability to extract that information from environments containing multiple competing streams, and potentially much louder background noise. Further, the delicate machinery of the inner ear needs to sustain very intense signals (reaching as high as 120 dB) without sustaining immediate and irreparable damage. There are many indications that the efferent neurons serve as a complex gain control mechanism for hearing. While their mechanisms and impact are far from fully understood, efferents are believed to play an important role in maintaining the integrity of hearing and fine-tuning the detection properties.
While efferent effects have been explored in vivo and shown to have a significant and multi-faceted impact on hearing, thus far there has been no direct exploration of how efferent activity impacts the mechanical sensitivity of the hair bundle. The active and nonlinear response of the bundles has been proposed to be subject to a gain control mechanism that tunes their response to enhance or reduce the sensitivity in response to external input. However, a clear experimental manifestation of this hypothesis has previously not been obtained.
We showed that efferent activity leads to significant changes in the mechanical response already at the level of the hair bundle. First, we showed that efferents exert a strong impact on the innate bundle oscillations, increasing the oscillation frequency and decreasing the amplitude. The effect was reversible under all the stimulus protocols tested, and was abolished when a pharmacological blocker of the ACh receptor was introduced into the perilymph solution.
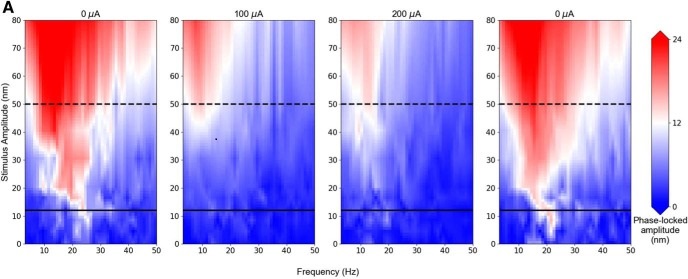 Figure 3. Receptive field maps of a hair cell were obtained
with and without efferent stimulation. Each plot was constructed by
mechanically driving the bundle at 24 frequencies (3-50 Hz in 2 Hz
increments) with 10 mechanical stimulus amplitudes (0 to 80 nm). The
first and last panels represent measurements obtained in the absence
of efferent stimulation. The second and third panels represent the
mechanical response of the bundle measured while the efferent
neurons were stimulated with pulse trains of 100 and 200 μA
amplitudes, respectively.
Figure 3. Receptive field maps of a hair cell were obtained
with and without efferent stimulation. Each plot was constructed by
mechanically driving the bundle at 24 frequencies (3-50 Hz in 2 Hz
increments) with 10 mechanical stimulus amplitudes (0 to 80 nm). The
first and last panels represent measurements obtained in the absence
of efferent stimulation. The second and third panels represent the
mechanical response of the bundle measured while the efferent
neurons were stimulated with pulse trains of 100 and 200 μA
amplitudes, respectively.
Next, we tested the sensitivity of the hair bundle under different levels of efferent stimulation. Full maps of the hair bundle response were obtained, showing the characteristic shape and properties of an Arnold Tongue. It shows the peak sensitivity of the hair bundle, at its characteristic frequency, and its nonlinear dependence on the stimulus amplitude. To determine the impact of efferent neurons, we measured these receptive field maps, both in the presence and absence of efferent activation. Under efferent stimulus, the resp onse was clearly and strongly reduced, across the full range of amplitudes applied (Figure 3). Increasing efferent stimulation increased the effect, which was fully reversible when the efferent activation is removed. The efferent feedback therefore exerts a direct effect already at the most peripheral level of detection, that of mechanical responsiveness of the bundle, affecting its very compliance to deflection. This is an important step towards unraveling the mechanism of how higher order processing in the brain affects the gain of amplification of hair cells.
Bifurcation theory and hair cell dynamics
A long-open question in the field of auditory neuroscience is how the inner ear achieves its remarkable sensitivity in the presence of ambient noise. Nonlinearity of the response is closely linked to the presence of an active process, by which the hair cell can amplify displacements induced by the incoming sound waves. Under in vitro conditions, hair cell bundles of certain species can exhibit spontaneous limit cycle oscillations, which require an expenditure of energy by the cell. These large-amplitude noisy oscillations can readily synchronize to applied stimuli, and constitute one potential mechanism of active amplification.
Hair bundle motility has been described with dynamic systems theory. One proposal is that a hair bundle is poised near a Hopf bifurcation, a critical point separating the quiescent state from spontaneous limit cycle regime. As the control parameter tunes the system toward or away from the bifurcation, it could modulate its amplification, frequency selectivity, occurrence of active motility, etc.
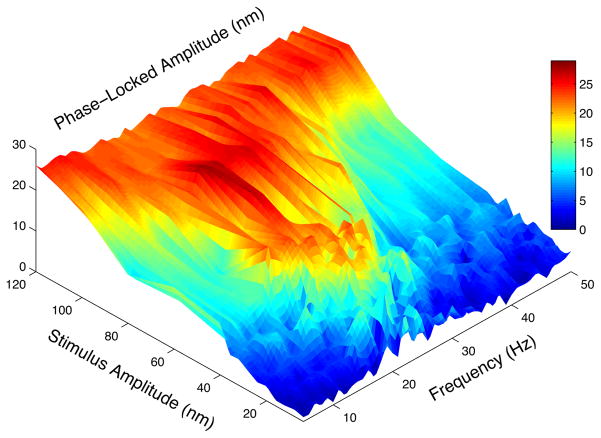 Figure 4. Phase-locked component of the hair bundle response. Stereociliary bundles were deflected from 5-50 Hz, and from 4-120 nm amplitudes.
Figure 4. Phase-locked component of the hair bundle response. Stereociliary bundles were deflected from 5-50 Hz, and from 4-120 nm amplitudes.
In prior studies, we measured how an oscillatory bundle phase-locks to an applied signal, across the full physiological range of frequencies and amplitudes (Figure 4). The measured Arnold Tongue – region of phase space where the bundle is entrained by the signal - was compared to that obtained from a simple numerical model and shown to exhibit a rich bifurcation diagram. The Hopf bifurcation, Saddle node bifurcation on an invariant circle, and the Bogdanov-Takens bifurcation, we found to be consistent with data obtained in different regimes. Our future entails combining these findings with control exerted by efferent neurons – the dynamical feedback system conveying information from the brain – to tune a hair cell in different bifurcation regimes and thus exhibit different detection characteristics.
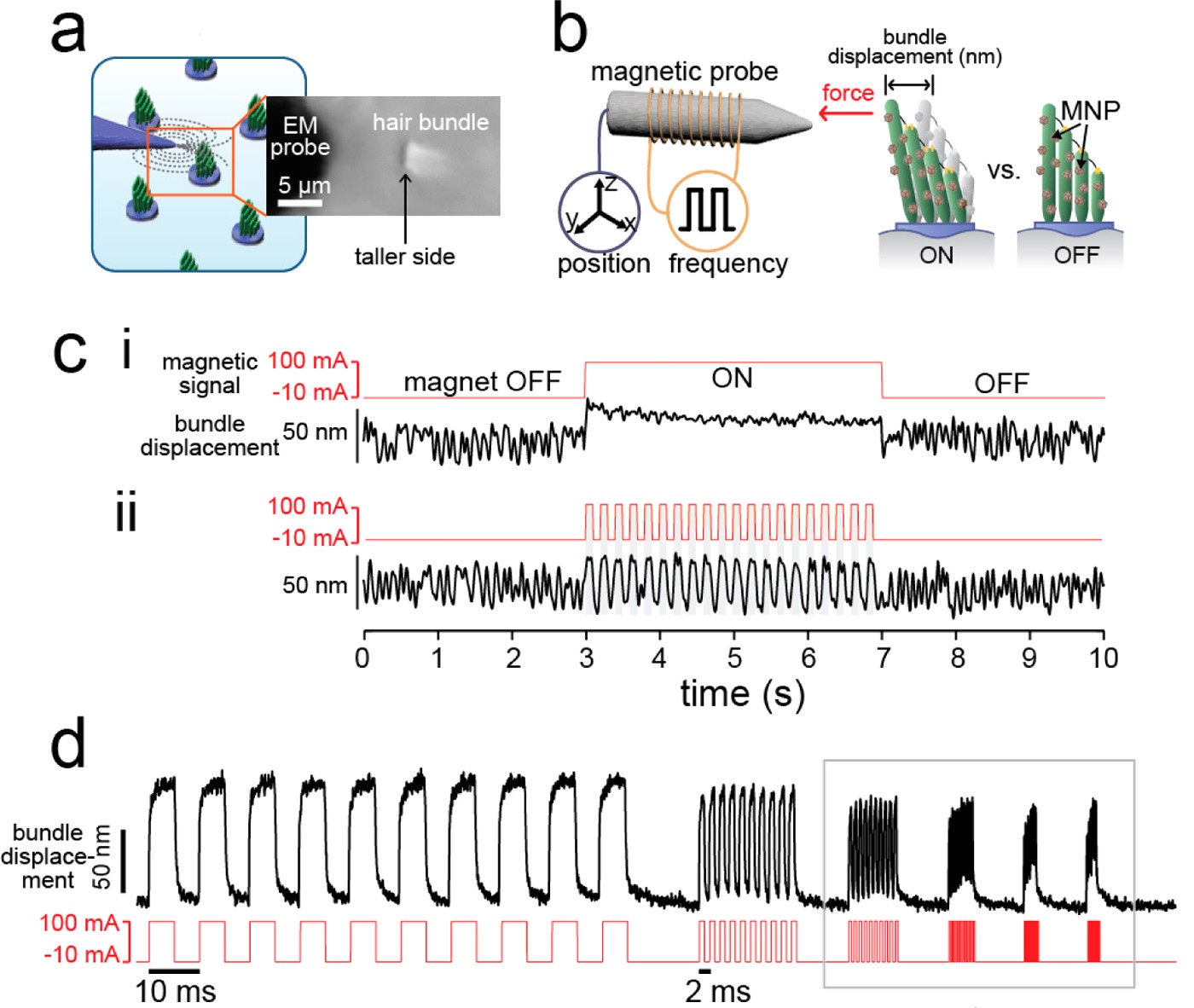
Magnetic nanoparticle actuation for probing temporal resolution
To explore higher-order synchronization between a hair cell and the applied signal, we used magnetic nanoparticles driven by an electromagnet to actuate the hair cells (Figure 5). Our data indicate that the evoked response shows extensive regimes of high-order mode-locking. Surprisingly, the measured Arnold Tongues show significant areas of overlap between different synchronization modes, with the hair bundle intermittently flickering between different winding numbers. We hypothesized that the transitions between the synchronization regions could in fact aid in the detection of higher frequency signals. In particular, we proposed that an ensemble of such oscillators would serve as a highly sensitive broadband detector. Future work entails connecting these findings to the work on chaotic dynamics.